重读经典：Word2Vec如何通过“简化”撬动了整个NLP世界？

摘要: 2013年，一篇名为《Efficient Estimation of Word Representations in Vector Space》的论文横空出世，它提出的构成Word2Vec核心思想的CBOW和Skip-gram架构，彻底改变了我们让机器理解语言的方式。本文将带您重温这篇里程碑式的著作，探讨其核心思想：为何一个看似更“简单”的模型，反而能发现语言中令人惊叹的深层结构？

原文链接：https://arxiv.org/abs/1301.3781

~~注：为了无障碍理解这篇论文，阁下可能需要先理解文末前置知识中提到的一些基本概念。~~

问题的根源：昂贵的“理解”

在Word2Vec出现之前，自然语言处理（NLP）领域长期面临一个难题：如何让计算机理解词语之间的关系？传统方法如One-hot编码，将每个词视为一个独立的符号，这使得“国王”和“女王”在模型眼中毫无关联。

as these(notion of words) are represented as indices in a vocabulary

虽然当时先进的神经网络语言模型（NNLM）已经可以通过“分布式表示”（Distributed Representation）将词语学习为低维、稠密的向量（即词向量），并在一定程度上捕捉到语义相似性。但这些模型通常包含一个或多个复杂的非线性隐藏层。这个隐藏层是模型强大表达能力的核心，却也成为了巨大的计算瓶颈。其复杂度，特别是Hidden Layer的计算~~（N×D×H part）~~，使得在数十亿词级别的海量数据集上训练模型变得不切实际。简单来说，当时的“理解”非常昂贵，以至于我们无法用足够多的数据去“喂养”它。

The main observation from the previous section was that most of the complexity is caused by the non-linear hidden layer in the model

解决方案：大道至简的两个模型

面对上述瓶颈，Mikolov和他的同事们提出了一个颠覆性的思路：
能不能用一个更简单的模型，来换取在更大规模数据上训练的能力？
于是，他们大胆地移除了计算成本高昂的非线性隐藏层，从而极大地降低了计算复杂度。
答案就是本文提出的两个核心架构：CBOW 和 Skip-gram。基本可以认为，这两个模型就是后来广为人知的Word2Vec。

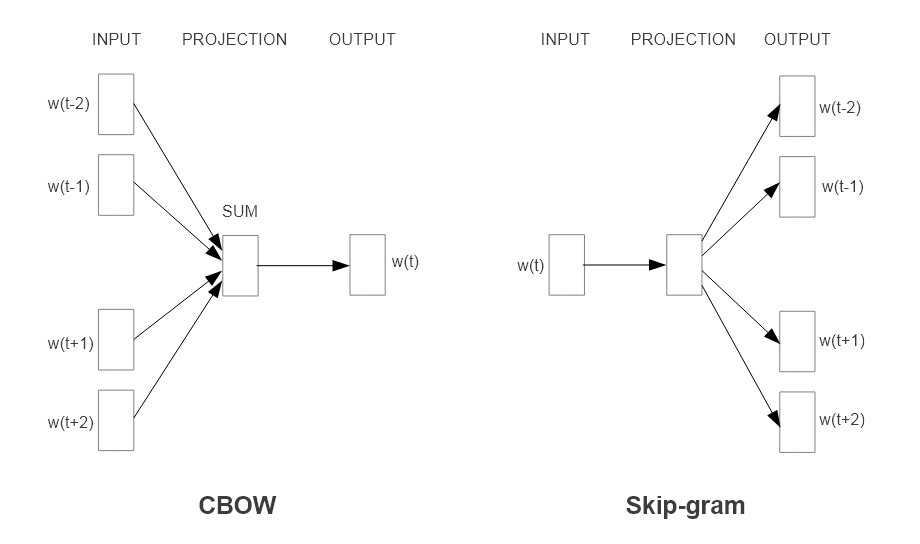
Continuous Bag-of-Words (CBOW)

任务：根据上下文（周围的词）来预测中心词。
做法：将目标词周围N个词的向量从投影矩阵~~(一个巨大的查询表，每一行即为一个词的向量)~~中取出，然后直接对它们进行求和平均，形成一个汇总的上下文向量，并用这个向量去预测中心词。因为忽略了上下文的词序，所以被称为“词袋”（Bag-of-Words）模型。
特点：多对一的预测，训练速度更快，对高频词效果更好。

Continuous Skip-gram

任务：与CBOW相反，它根据当前的中心词来预测其上下文。
做法：将中心词的向量作为输入，去预测其前后一定范围（窗口C）内的多个上下文词语。并且通过将窗口的大小设计为固定范围的随机数，便可实现统计意义上的对远端词语进行更少采样，从而给予近处上下文更高的权重，这或许可以被看作是一种朴素的、非动态学习的“注意力”思想的雏形。
特点：一对多的预测，训练时间更长，但能学习到更好的低频词表示，在大型语料上表现通常更优。论文的实验结果（如Table 3）也证实了这一点，Skip-gram在语义准确性上以55%对24%的巨大优势超过了CBOW。
~~和CBOW不同，Skip-gram的训练模式可能会有些难以理解，容易产生歧义，具体讲解可见 Skip-gram训练机理~~

这种简化带来的好处是惊人的。计算复杂度从NNLM的Q = N×D + N×D×H + H×V 急剧下降到CBOW的 Q = N×D + N×log_2(V) 和 Skip-gram的 Q = Cx(D + D×log_2(V))。正是这种效率上的巨大飞跃，使得在一天之内处理完16亿词的语料成为可能，也为接下来那个“魔法般”的发现奠定了基础。

注：这里提到的Q基本上可以理解为模型一次预测所涉及的参数量;

Similar to [18], to compare different model architectures we define first the computational complexity of a model as the number of parameters that need to be accessed to fully train the model.

注：此外，V到log_2(V)的变化是通过使用词汇的二叉树表示实现的，也就是说这对于NNLM的复杂度优化也是有用的，但是优化完之后，性能瓶颈在NxDxH, 仍然没有消失。

With binary tree representations of the vocabulary, the number of output units that need to be evaluated can go down to around log2(V ). Thus, most of the complexity is caused by the term N × D × H.

惊人的发现：向量空间中的线性关系

如果说高效的模型是这篇论文的“肌肉”，那么它揭示的向量线性关系就是其“灵魂”。论文最令人振奋的发现是，通过上述简单模型在海量数据上训练出的词向量，不仅仅是让“猫”和“狗”在空间中彼此靠近，更是捕捉到了词语之间丰富、可量化的类比关系（Analogy）。

这种关系可以通过简单的向量代数运算来揭示。最经典的例子莫过于：

这个等式石破天惊，它表明词向量空间中蕴含着抽象的语义维度，例如“性别”、“皇室”等。从“国王”的向量中减去“男人”的向量，相当于抽离出“男性”这个概念，保留了“皇室权威”等特征；再加上“女人”的向量，就将这个“皇室权威”的特征赋予了女性，最终得到的向量在空间中将接近“女王”对应的向量。~~在这个空间中，词向量的距离可以表示语义的相似度。~~

为了系统性地验证这一发现，作者团队专门构建了一个包含语义(Semantic)和语法(Syntactic)类比问题的综合测试集~~Semantic-Syntactic Word Relationship test set~~。示例：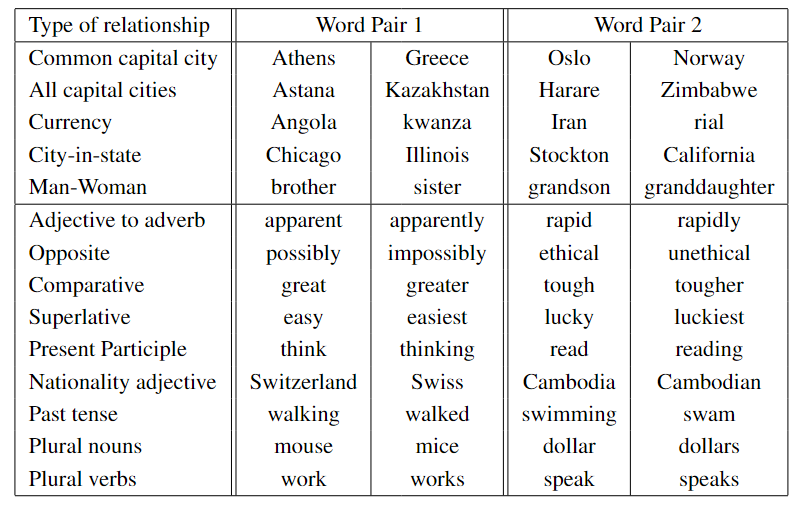

语义类比: Athens is to Greece as Oslo is to? (Norway)
语法类比: apparent is to apparently as rapid is to? (rapidly)

注: 在实操上，可以通过上述向量运算得到结果向量，最后在整个词汇表的向量中，寻找与这个结果向量距离最近的词向量，这个词就是模型的答案——论文中使用的距离度量为“余弦距离”。
在下以为，若所有词向量都预先进行归一化（使其长度为1），那么计算成本高昂的余弦距离就可以被简单的“向量点积”所替代。在单位球面上，按点积大小排序等同于按欧氏距离排序，但计算效率更高。ps: 单位球面上，

实验结果（论文中的Table 3, 4; 6）雄辩地证明，CBOW和尤其是Skip-gram模型，在这类任务上的准确率远超当时更复杂的NNLM和RNNLM模型，同时训练成本大幅降低。
准确率：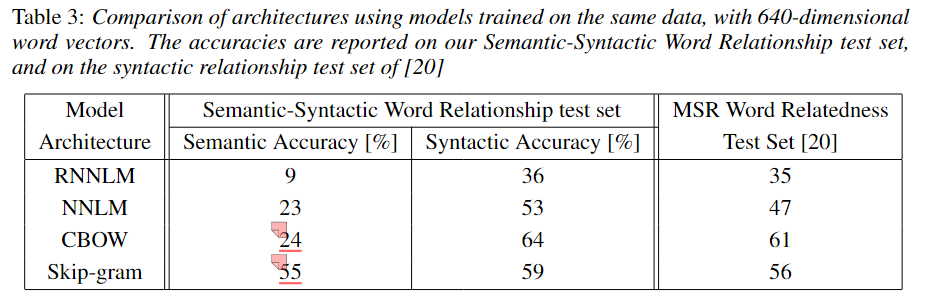

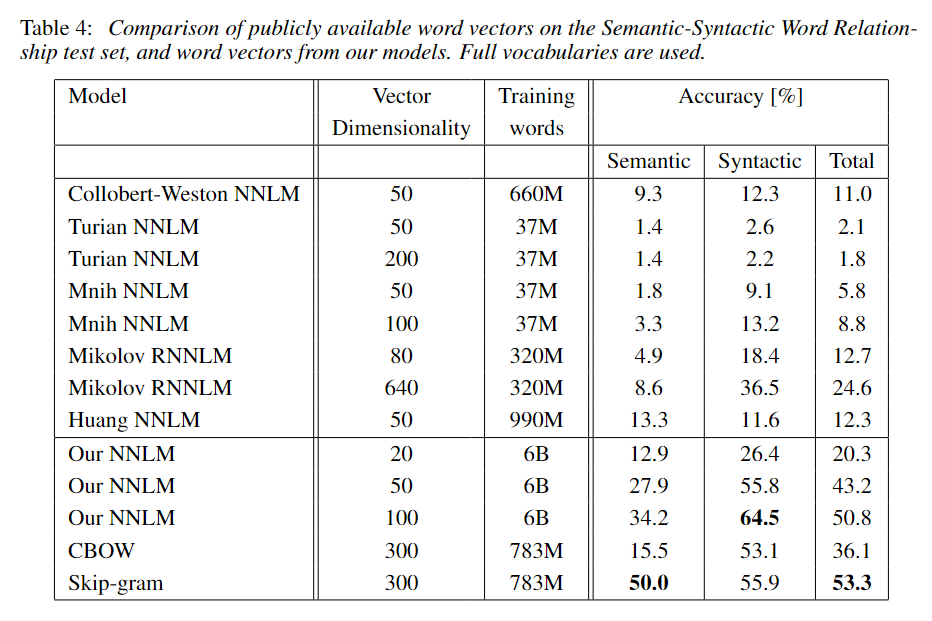
训练成本：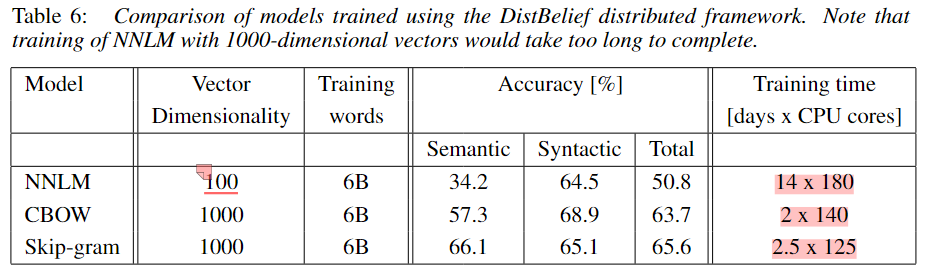

历史回响：前沿性

它被推翻了吗？

思想从未被推翻，反而成为了基石。 “将词语映射到稠密向量空间中，通过无监督学习捕捉其语义”这一核心思想，已经成为整个现代NLP的奠基性观念之一。

它还是最前沿吗？

具体技术已演进，但思想永存。

Word2Vec的局限在于它生成的是静态词向量~~(训练得到一个固定的词向量查询表)~~，对于一个token只有一个表示，无法处理一词多义问题（例如”bank”的“银行”和“河岸”两个含义共享同一个向量）。而当代的SOTA（State-of-the-Art）技术，如BERT、GPT等基于Transformer的模型，生成的是动态的、上下文相关的词向量。它们能根据句子语境为同一个词生成不同的表示，极大地提升了语义捕捉的精度。大体上应该可以理解成：输入句子之后，句子中的所有词首先经过一层类似于Word2Vec的初始嵌入，然后在经过注意力机制处理后，再输出每个词最终的词向量
同时，CBOW由于其BOW的模型，缺乏对位置的建模； Skip-gram的位置概念也非常模糊，并未显式建模。
此外，word2vec模型本身并未提供直接获取整个句子向量的有效方法，通常采用的“词向量平均”策略会丢失重要的语序和语法信息。
然而，即便在今天，Word2Vec因其高效、轻量的特性，仍在学术研究和工业界中扮演着重要角色，甚至就连它被诟病的无法应对一词多义的问题有时也是一种优势——因为它可以得到一个稳定的向量训练结果，若要知晓某个词的向量，在向量表~~(投影矩阵)~~中直接查询即得。

杂谈

《Efficient Estimation of Word Representations in Vector Space》是一篇充满“反直觉”智慧的论文。它告诉我们，有时最优雅的解决方案并非来自更复杂的模型，而是来自对问题本质的深刻洞察。通过极致的简化，Word2Vec将计算力从复杂的模型结构中解放出来，投入到对海量数据的学习中，最终发现了语言本身蕴含的、令人着迷的数学之美。这不仅是一次技术的胜利，更是一次思想的胜利。

一些可能容易迷惑的点：

最终产物

虽然Word2Vec在训练时的确利用了上下文，但请注意，训练的最终产物是一个固定的查询表（即投影矩阵 W）。训练结束后，无论“bank”出现在什么新的句子中，我们去使用它的词向量时，做的动作仅仅是查表——从矩阵W中把“bank”对应的那一行向量取出来。这个向量是一次性生成、全局固定的，所以它是“静态”的、“上下文无关”的。上下文信息在训练时被“蒸馏”进了这个固定的向量里，但在使用时，新的上下文不起作用。

实际上这种方式训练出来的是一个既能进行嵌入又能进行预测的模型——正是因为有预测的能力，所以才能计算损失进行反向传播，从而不断调试投影矩阵，进而得到较好的词向量表示，也就得到了一个较好的嵌入模型。这或许也算是这类自监督学习（Self-supervised Learning）模型的训练哲学吧。我们并不真正关心模型预测得有多准，这个“预测任务”只是一个“借口”。我们真正的目标是，在完成这个任务的过程中，强迫模型学习到有意义的中间表示——也就是那个高质量的“投影矩阵”（词向量）

共享投影层的说法

论文在介绍模型架构时提到的共享投影层(using a shared projection matrix)可能会让人感到困惑。在下认为，这里的共享主要指的是对于上下文窗口的不同位置，使用是同一个投影矩阵进行映射；对比的是上下文窗口的每个位置分别维护不同的投影矩阵。除此之外，在CBOW中，作者还做了一个更激进的共享——投影后所处的空间位置也进行共享：输入的N个词向量在查找到之后，将被直接平均（Average）成一个单独的D维向量，空间位置信息被彻底抹除；对比在NNLM中，查到的向量会被拼接成N*D维的长向量

Note that the weight matrix between the input and the projection layer is shared for all word positions in the same way as in the NNLM.

Skip-gram训练机理

要理解Skip-gram，首先需要明确其核心精髓——它不追求单个预测的精准度 ~~预测任务只是一个“借口”，我们真正的目标是在这个过程中“锤炼”出优秀的词向量~~

CBOW是将多个上下文单词加起来，然后用聚合后的向量一次性去预测中心词，每次训练就聚焦一次：目标词和使用聚合向量预测目标词的概率
而Skip-gram, 则从中心词出发，和上下文窗口C中的所有词分别组成一个独立的训练样本对，每次训练就聚焦C次：这一次的目标词和使用中心词向量预测该目标词的概率
例如：假设我们的句子是I am a fool, 窗口大小C=1, 当前处理的中心词是a
则形成两个独立的训练样本对：

a -> am
a -> fool
所以模型会训练两次，一次输入a，使用预测出am的概率计算损失；一次输入a，使用预测出fool的概率计算损失~~在使用层级Softmax的时候损失计算可能没有这么简单，但本质不变~~
在反向传播的时候，不仅会调整输出层的权重，更重要的是也会调整a的词向量，从而不断拉扯a的词向量，让它更符合上下文语境

计算复杂度

论文中给出的计算复杂度公式乍一看可能有些吓人。但根据论文定义，它估算的主要是训练时需要访问的参数数量，理解起来并不复杂。下面我们进行简要拆解：

NNLM: Q = N×D + N×D×H + H×V

N×D：这部分代表从输入层到投影层的计算。将N个上下文单词（通常是one-hot）通过投影矩阵映射为N个D维向量，再拼接成一个N×D维的向量。因为涉及到了投影矩阵中的N行，所以对应参数量为N×D
N×D×H：这是计算瓶颈，代表从投影层（N×D维）到非线性隐藏层（H维）的全连接计算。~~在这篇论文的语境下，应该是默认其所对比的NNLM为仅拥有单层非线性隐藏层的经典模型~~
H×V：代表从隐藏层（H维）到巨大无比的输出层（V维，V是词汇表大小）的全连接计算。

CBOW: Q = N×D + D×log₂(V)

N×D：与NNLM类似，查询N个上下文单词的D维向量。
D×log₂(V)：模型移除了N×D×H的隐藏层。将N个词向量平均后得到仅仅一个D维向量，直接用它来预测输出。同时，输出层使用层序Softmax（Hierarchical Softmax）这种技巧，将原本D×V的计算量降维打击至D×log₂(V)，因为它只需要在一个二叉树（深度约log₂(V)）上做一系列二分类判断，而不是在全部V个词上计算概率。所以这个技术对于NNLM同样适用，理论上上面NNLM的复杂度也可以优化，但是不影响CBOW和Skip-gram仍然远比它快。

Skip-gram: Q = C×(D + D×log₂(V))

D：输入只有一个词，查询其D维向量。
D×log₂(V)：用这个D维输入向量，去预测一个上下文单词。与CBOW一样，也用了层序Softmax优化。
C×(...)：因为Skip-gram模型需要对一个输入词，预测其周围的C个上下文单词，所以上述过程需要重复C次。

一言以蔽之：Word2Vec的效率革命，主要来自（1）砍掉N×D×H的隐藏层和（2）用log₂(V)复杂度的层序Softmax替换V复杂度的普通Softmax。

关于层序Softmax的使用，感兴趣的话可以作者参考引用的这几篇论文

T. Mikolov, A. Deoras, D. Povey, L. Burget, J. Cˇ ernocky ́. Strategies for Training Large Scale Neural Network Language Models, In: Proc. Automatic Speech Recognition and Understanding, 2011.
A. Mnih, G. Hinton. A Scalable Hierarchical Distributed Language Model. Advances in Neural Information Processing Systems 21, MIT Press, 2009.
F. Morin, Y. Bengio. Hierarchical Probabilistic Neural Network Language Model. AISTATS, 2005.

前置知识

词的表示方法：从One-hot到分布式表示
- One-hot：想象一个词典有10万个词，那么“apple”这个词可能被表示成一个10万维的向量，其中只有对应“apple”的位置是1，其余全是0。这种方式无法体现词与词之间的关系。
- 分布式表示 (Distributed Representation)：与One-hot不同，它用一个稠密的、低维度的向量（例如300维）来表示一个词。向量中的每一个维度都代表了词语的某种潜在特征。这篇论文的核心就是如何高效地学习这种表示。
全连接层
- 一个全连接层包含一个权重矩阵W和一个偏置向量b。当输入一个向量x时，输出为y = Wx + b。
神经网络语言模型 (NNLM) 的基本结构
- 阁下只需要大致了解它通常包含输入层、投影层、隐藏层和输出层。
- 其中投影层的概念可能会让人有点陌生，但对于理解本文思路又至关重要，所以这里在下简要介绍基本原理
  - 您可以把它想象成一个巨大的查询表。输入层的一个词就像一个开关，正好选中表中的某一行。这一行，就是一个低维、稠密的向量，它就是那个词的分布式表示。因此，这个投影层矩阵本身，在训练结束后，就成为了我们最终想要的“词向量词典”。
向量空间与相似度
- 当词语被表示为向量后，我们就可以在多维空间中计算它们之间的距离（如余弦距离）。距离越近，代表这两个词语的语义或用法越相似。

References

[1] T. Mikolov, K. Chen, G. Corrado, and J. Dean. Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781, 2013.

少女祈祷中... (◕ᴗ◕✿)